توضیحات
الگوریتم کلونی مورچه(ACO ) الهام گرفته شده از مطالعات و مشاهدات بر روی کلونی مورچه-هاست. هدف این الگوریتم، یافتن پاسخ های نزدیک به پاسخ اصلی می باشد که در این راه از تولید فرمون های مصنوعی و شبیه سازی رفتار گروهی مورچه ها و ارتباطات غیرمستقیم آنها استفاده می-کنند.
الگوریتم ACO یک خانواده از مجموعه الگوریتم های فراابتکاری می باشد که برای حل طیف وسیعی از مسایل سخت(TSP,QAP,…) به کار گرفته می شود ( Dorigo, et al., 2002). دراین بخش به معرفی منشاء این الگوریتم، ساختار کلی و اعضای اصلی این خانواده پرداخته می شود.
3-7-1- منشاء زیست شناسانه الگوریتم کلونی مورچه ها
یکی از مسائلی که حشره شناسان روی آن تحقیق کرده اند این است که چگونه موجوداتی نابینا نظیر مورچه ها می توانند مسیر کوتاهتر از آشیانه به طرف منبع غذا و بالعکس را بیابند؟ نتیجه این تحقیقات این بود که یک مورچه خود به تنهایی در مسیر های کاملا تصادفی حرکت می کند و در حالیکه این امر در مجموعه ای از مورچه ها صدق نمی کند. مجموعه مورچه ها به هنگام حرکت به واسطه محیط تبادل اطلاعات می کنند. هر مورچه به هنگام حرکت مقداری فرومون (در مقادیر متفاوت) بر روی زمین از خود بر جای می گذارند. مورچه ها از راه استشمام این ماده شیمیایی برای تبادل اطلاعات آن ها در مورد مسیرها استفاده نموده و مسیری مناسب را انتخاب می کنند.
در مجموعه ای از مورچه ها، مورچه ای که با ردپای فرومونی مواجه می شود، می تواند آنرا شناسایی کرده و تصمیم بگیرد که کدام مسیر را با احتمال بیشتری انتخاب کند. همین مورچه با حرکت در مسیر فرومون دار، آنرا با فرومون ترشحی خودش تقویت می کند. این رفتار جمعی مورچه ها سبب ایجاد رفتار خودشتاب دهنده شده و همین امر سبب می شود تا مورچه های بیشتری مسیر مناسب را انتخاب نمایند. فرایند خود شتاب دهنده فرایندی است که خودش راتقویت می کند و همین امر سبب هم گرایی سریع الگوریتم می شود. به دلیل افزایش تردد در مسیر مناسب تر، این مسیر بعد از مدت زمان گذرایی توسط فرایند زنجیر وار بازخورد مثبت تقویت شده و بیشتر مورچه ها آنرا برای حرکت انتخاب می نمایند. این رفتار طبیعی مورچه های طبیعی منشا الگوریتم های مورچگان می باشد ( Dorigo, et al., 2004).
فرومون ریزی و دنبال کردن آن توسط تعدادی از گونه های خاص مورچه ها در شرایط کنترل شده آزمایشگاهی، توسط محققین زیادی انجام گرفته است. یکی از این آزمایشهای با ارزش بوسیله دنوبورگ و همکارانش طراحی و انجام شده است. (Goss, et al., 1989; Deneubourg, et al., 1990) در این آزمایش که به آزمایش پل دوگانه معروف می باشد، از یک اتصال دهنده بین غذا و لانه مورچه ها استفاده کرد( Dorigo, et al., 2004).
شرایط آزمایشگاهی که در شکل 3-4 نشان داده شده است، را در نظر بگیرید. در قسمت a از این شکل مورچه ها در مسیری که از منبع غذایی A به طرف آشیانه E و بالعکس در حال حرکت می باشند، نشان داده شده اند. ناگهان مانعی بر سر راه مورچه ها قرار گرفته و مسیر بسته می شود. در نقطه B مورچه هایی که از A به B حرکت می کنند (و یا در نقطه D مورچه هایی که در مسیر مخالف حرکت میکنند) بایستی تصمیم بگیرند که به سمت چپ یا راست حرکت نمایند.(قسمت b در شکل3-4). انتخاب مسیر توسط مورچه ها به میزان فرومونی که در هر مسیر وجود دارد وابسته است. هر چه میزان فرومون بیشتر باشد آن مسیر با احتمال بیشتری انتخاب خواهد شد. اولین مورچه ای که به نقطه B و یا D می رسد، با احتمال یکسان به سمت چپ یا راست حرکت میکند. (در صورتیکه هیچ فرومونی در سمت چپ یا راست موجود نباشد که این گونه فرض شده است) از آنجایی که مسیر BCD کوتاهتر از مسیر BHD می باشد، اولین مورچه ای که از این مسیر عبور کند زودتر از مورچه ای که از مسیر دوم حرکت کرده است به غذا می رسد(قسمت c شکل3-4).
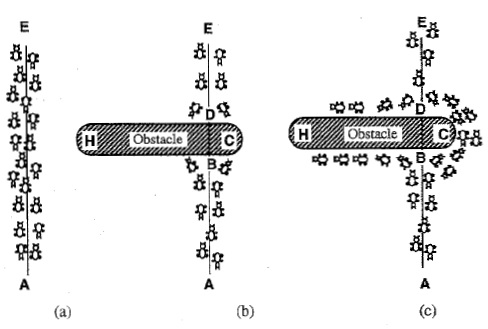
شکل 3 4: رفتار مورچه های واقعی در حالت عادی ( Dorigo, et al., 1996)
همین امر در مورد مورچه هایی که از منبع غذایی به طرف آشیانه در حرکت می باشند، نیز صادق می باشد. لذا مورچه ای که مسیرBCD را انتخاب کرده است سریعتر از مورچه ای که مسیر BHD را انتخاب نموده به مقصد رسیده و سبب تقویت فرومون مسیر کوتاهتر می شود. در واقع با گذشت زمان، تعداد مورچه هایی که در واحد زمان مسیرBCD را انتخاب می کنند از تعداد مورچه هایی که مسیر دوم را انتخاب می کنند بیشتر می شود. این امر سبب می شود که میزان فرومونی که در مسیر کوتاهتر انباشته می شود، از میزان فرومونی که در مسیر طولانی تر می باشد، بیشتر شده و مورچه ها مسیر کوتاهتر را با احتمال بیشتری انتخاب نمایند. نتیجه اینکه در مدت زمان کوتاهی تمام مورچه ها مسیر کوتاهتر را برای رسیدن به هدف انتخاب می کنند ( Dorigo, et al., 1996).
مجموعه الگوریتم های بهینه یابی مورچه ها(ACO) جزو جدیدترین رویکردهای ابتکاری جهت حل مسائل بهینه یابی ترکیبی مشکل می باشند. این الگوریتم ها ترکیبی از محاسبات غیرمتمرکز ، بازخورد مثبت و الگوریتم های ابتکاری ساخت گرا می باشند که هر کدام از این بخش ها وظایف مشخصی را به عهده دارند. بخش محاسبات غیر متمرکز الگوریتم مورچه ها، از هم گرایی سریع و گرفتار شدن الگوریتم در نقاط بهینه محلی جلوگیری می کند. بخش بازخورد مثبت، وظیفه شناخت و کشف سریع جواب های مناسب و خوب را بر عهده دارد و الگوریتم های ابتکاری ساخت گرا نیز به دنبال یافتن جواب های اولیه شدنی هستند و این جواب ها را در تکرار-های متوالی پیدا و به جواب تهی اولیه اضافه می کنند تا جواب کامل ایجاد شود (سپهری و همکاران، 1386). ایده اصلی این مجموعه از الگوریتم ها، بر جا ماندن ماده فرومون به عنوان ردپا در دنیای واقعی مورچه ها می باشد. مجموعه کلیه الگوریتم هایی که از ایده مسیریابی مورچه-های واقعی برای حل مسائل استفاده می کنند، نظیر الگوریتم های AS ، MMAS ، ACS، Ant-Q و AntNet به الگوریتم های بهینه یابی مورچه ها معروف می باشند (سپهری و همکاران، 1386) ( Dorigo, et al., 2004).
کاربردهای الگوریتم های مورچگان به دو دسته کلی مسائل بهینه یابی ترکیبی استاتیک و دینامیک تقسیم می شوند. مسائل استاتیک مسائلی می باشند که ساختار آنها در حین حل مسئله تغییر نمی کند؛ نمونه ای از این نوع مسائل مسئله فروشنده دوره گرد کلاسیک متقارن می باشد که در آن موقعیت و فاصله بین شهر ها در حین حل مسئله تغییری نمی کند. مسائلی دینامیک می باشند که ساختار آنها در حین حل مسئله تغییر می کند؛ مسیر یابی در شبکه های ارتباطی نمونه ای از این نوع مسائل می باشد. محدوده کاربرد مجموعه الگوریتم های مورچه ها بسیار وسیع می باشد. این مجموعه از الگوریتم ها می توانند برای حل تمام مسائل بهینه یابی گسسته مورد استفاده قرار گیرند. مسائل بهینه یابی گسسته مسائلی هستند که فضای جواب آنها گسسته می باشند. الگوریتم های مورچه ها از پایداری زیادی برخوردار بوده و با تغییرات بسیار کمی می توانند برای انواع مسائل مختلف بهینه یابی مورد استفاده قرار گیرند. پایداری یک الگوریتم به میزان توانایی آن الگوریتم برای حل انواع مختلف مسائل بهینه یابی گفته می شود ( Dorigo, et al., 2004)
در حال حاضر مجموعه الگوریتم های ACO توسعه بسیار زیادی یافته اند و از آنها در مقیاس بسیار وسیعی جهت حل مسائل پیچیده بهینه یابی استفاده می شود. نمونه ای از مسائلی که با استفاده از این الگوریتم ها حل شده اند، عبارتند از: مسئله تخصیص درجه دو، مسیریابی وسایل نقلیه، زمان بندی، مسیریابی در شبکه های ارتباطی، مسئله سفارش متوالی،، بهینه سازی چند هدفه، مکانیابی و تخصیص. (سپهری و همکاران، 1386)
3-7-2- ساختار مسائل قابل مدلسازی برای حل با مجموعه الگوریتم های مورچه
الگوریتم مورچه ها نیز به طور عمده برای حل مسائل بهینه یابی گسسته ای مناسب ترند که بتوان قسمت های زیر را برای آن مسئله خاص مشخص و تبیین نمود:
• مجموعه متناهی از نقاط C={c1,c2,c3,…,cNc}
• مجموعه متناهی L از یالهای بین اعضای C که C زیر مجموعه ای از حاصل ضرب کارتزینC*C می باشد.
• تابع هزینه Jcicj=J(lcicj ,t) که بای هر یال L lcicj نسبت داده می شود که این هزینه می تواند تابعی از طول مسیر باشد.
• مجموعه ای متناهی از محدودیت های Q=Q(C,L) که این محدودیت ها بروی مجموعه های C و L تعریف می شوند. محدودیت ها می توانند تابعی از شرایط مسئله باشند.(مثلا درTSP باید عامل از تمام شهرها عبور کند تا یک دور حساب شود یا در تحقیق پیش رو قید مساحت را داریم)
• حالات مسئله که به صورت توالی S={c1,c2,c3,…,ck} روی اعضاء مجموعه C (یا L) تعریف می شود. با در نظر گرفتن S به عنوان مجموعه تمامی توالی های ممکن، زیر مجموعه ای از S که در تمامی محدودیت های Q صدق نماید مجموعه تمامی توالی های شدنی خواهد بود که این مجموعه را با Ŝ نشان می دهیم. اعضای مجموعه Ŝ حالات شدنی مسئله می باشند.
• یک جواب Ψ عضوی از Ŝ می باشد.
• هزینه JΨ(L,t) که به هر جواب نسبت داده می شود، تابعی از تمامی هزینه های Jcicj متناظر با یالهای موجود در جواب می باشد ( Dorigo, et al., 2004).
3-7-3- شبیه سازی رفتار مورچه ها در ACO
مورچه های مصنوعی رویه های احتمالی جواب می باشند که بوسیله حرکت بروی گراف G=(C,L) وظیفه خود را انجام می دهند. البته این حرکت به صورت دلخواه و اختیاری نیست؛ بلکه از یک خط مشی ایجاد جواب پیروی می کند.که این خط مشی تابعی از مجموعه محدودیت-های مسئله (Q) می باشد. بطور کلی مورچه ها تلاش می نمایند تا با حرکت بروی گراف مسئله جواب های شدنی را ایجاد نمایند. در نهایت جواب بهتر از بین جواب های شدنی انتخاب می شود.
برای اینکه مورچه ها به وظیفه خود عمل کنند؛ از دو نوع منبع اطلاعاتی استفاده می نمایند که یکی از این منابع مربوط به خود مورچه ها بوده و دومی منبعی خارج از محدوده کار مورچه می باشد. منبع اطلاعاتی مربوط به مورچه ها، فرومون می باشد. منبع اطلاعاتی دوم نیز اطلاعات خاص مسئله بوده و به اطلاعات ابتکاری معروف می باشد که بیانگر اطلاعات خاص مسئله مورد بررسی ( نظیر فاصله بین گره ها در مسئله TSP ) و یا اطلاعاتی در حین اجرای مسئله می باشد و همانطور که بیان شد منبع آن غیر از مورچه ها می باشد. برای استفاده مورچه ها از این منبع اطلاعاتی، آن ها به اعضای مجموعه های C ( یاL ) مقدار iȠ (یا ijȠ ) نسبت داده می شود که مرتبط با اطلاعات خاص مسئله می باشد. البته در اغلب اوقات Ƞ، هزینه و یا تخمینی از هزینه می باشد. در مسئله ای که هدف کمینه کردن هزینه می باشد، اطلاعات کاوشی عکس هزینه مسیر پیموده شده و یا هر پارامتر تعریف شده در مسئله می باشد.
در اغلب الگوریتم های ACO اجزای مختلف جواب بصورت تدریجی و احتمالی به جواب ناقص اضافه می شود. اضافه شدن احتمالی اجزای مختلف جواب به جواب تهی اولیه، به مورچه ها این اجازه را می دهد که مجموعه جواب های ممکن بسیاری را مورد بررسی قرار دهند. از طرفی استفاده از اطلاعات ابتکاری نیز مورچه ها را در یافتن جواب های بسیار خوب راهنمایی می نماید. مهمتر از همه، انتقال تجربه جستجوی مورچه های قبلی به مراحل بعدی جستجو، احتمال یافتن جواب های بسیار خوب را افزایش می دهد. در واقع این الگوریتم از بازخورد مثبت به عنوان یک راهبرد جستجو استفاده می کند ( Dorigo, et al., 2004).
تک تک عامل ها در الگوریتم ACO دارای ویژه گیهای زیر می باشند:
• هر مورچه بروی گراف G = (C,L) برای یافتن جواب های شدنی Ψ با کمترین هزینه حرکت می کند.
• مورچه k ام اطلاعات مسیری که تا به حال طی کرده است را در حافظه Mk خود ذخیره می کند که این حافظه برای ایجاد جواب های قابل قبول، ارزیابی کیفیت جواب های ایجاد شده و ردیابی دوباره مسیر طی شده جهت پخش فرومون مورد استفاده قرار می گیرد.
• چنانچه در یک حالت خاص هیچ کدام از شرایط پایان برقرار نباشد، مورچه با یک حرکت به حالت بعدی منتقل می شود و اغلب این حرکت به سمت حالات مطلوب تر می باشد.
• در هر مرحله تصمیم مورچه ها در مورد جهت ادامه حرکت، تصمیمی احتمالی است. این تصمیم احتمالی تابعی از میزان فرومون موجود بروی یالهای(یا گره های) پیشرو، اطلاعات خاص مسئله در آن مرحله و محدودیت های مسئله می باشد.
• هر مورچه زمانی رویه ایجاد جواب را متوقف می کند که حداقل یکی از شرایط اختتام مربوط به خودش برقرار باشد.
• زمانی که یک جز جواب ci به جواب فعلی اضافه می شود می توان میزان فرومون مرتبط با آن یال را به روز نمود ( Dorigo, et al., 2002).
• به محض اینکه جوابی ایجاد و کامل شد، می توان با استفاده از حافظه عامل ها مسیر طی شده توسط عامل را دوباره برگشته و میزان فرومون موجود بر روی اجزای مسیر را به روز نمود ( Dorigo, et al., 2004).
هر چند که مورچه ها به صورت همزمان و مستقل از یکدیگر حرکت می نمایند، ولی نتایج شدنی که حاصل می شود نتیجه همکاری بسیار نزدیک مورچه ها به واسطه تبادل اطلاعات می باشد. هر مورچه به هنگام عبور از یال (یا گره) خاصی، اطلاعات موجود بر روی آنرا که تجربه کلیه مورچه های قبلی رد شده از آن می باشد را خوانده، از آن برای تصمیم گیری استفاده کرده و در نهایت با به روز کردن فرومون تجربه خود را نیز به بدان می افزاید. این اطلاعات توسط مورچه-های بعدی که از آن یال (یاگره) رد می شوند، خوانده شده و این فرآیند ادامه پیدا می کند (سپهری و همکاران، 1386).
3-7-4- ساختار عمومی الگوریتم های ACO
رویه اصلی الگوریتم ACO به وسیله فعالیتهای برنامه ریزی شده ای مدیریت می شود که شامل:
• تولید و عمل مورچه های مصنوعی
• آپدیت فرومون
• در قسمت اول مجموعه ای از مورچه ها به صورت همزمان بر روی گراف مسئله از حالتی به حالت دیگر منتقل می شوند. مورچه ها برای حرکت بین حالات مختلف مسئله از رویه های احتمالی که در قسمت های قبل اشاره شد استفاده می کنند و در حین حرکت بر روی یالهای گراف به تدریج جواب هایی را ایجاد می نمایند. بعد از اینکه جوابی توسط مورچه ای ایجاد شد و یا حین ایجاد جواب توسط مورچه، جواب ایجاد شده مورد ارزیابی قرار گرفته و متناسب با کیفیت جواب، در مرحله بعد مقداری فرومون بر روی یالهای (یا گره های) عبوری ترشح می شود که این فرومون مورچه های بعدی را برای جستجو راهنمایی می کند.
• آپدیت فرومون مرحله ایست که فرومون مسیر دچار تغییر می شود. مقدار فرومون بر روی مسیر هم می تواند افزایش یابد، زمانیکه عامل فرومون را بر روی مسیر هایی(گره هایی) که از آنها عبور کرده قرار دهد؛ و یا اینکه فرومون را با تبخیر کاهش دهد. تبخیر فرومون رویه ایست که برای کاهش میزان فرومون بر روی یالها در طی زمان و جلوگیری از همگرایی سریع الگوریتم به جواب های بهینه محلی . در واقع این رویه نوعی فراموشی بخشی از تجارب مورچه های قبلی، برای ایجا امکان جستجوی نواحی و نقاط جدید در فضای حل مسئله می باشد ( Dorigo, et al., 2004)

















نقد و بررسیها
هنوز بررسیای ثبت نشده است.